Отдельно рассмотрим задачи A, B, H.
Задача B должна была быть очень простой, но краткость формулировки (здесь
исправлено) затруднила понимание того, из чего состоит последовательность
целых чисел. Конечно, из скоростей эльфов и дракона. Сколько эльфов неизвестно,
но у всех эльфов скорости одинаковые. Значит, надо читать числа до тех
пор, пока не встретятся два разных числа. Простое решение я подсмотрела у
команды Примашки:
int u,v;
cin >> u >> v;
while (u==v)
{
cin >> v;
}
cout << (v+u) / 2.0 << endl;
Первую точку можно выбрать n способами.
Каждую из следующих n–2 точек можно выбрать двумя способами, так как она должна
быть соседней с одной из ранее выбранных точек (иначе получится
самопересекающаяся ломаная). Поскольку начало и конец при таком подсчёте не
различаются, результат нужно разделить на 2. Следовательно, всего имеется
n·2n–2/2 = n·2n–3
ломаных.
Осталось вычислить степень двойки.
Остальные задачи были в составе контеста Третьей Всероссийской командной
олимпиады школьников по программированию (ВКОШП) 2002 года. Это задачи
B. Форум.
C. Три города (спасибо Илье Первакову, первому обратившему мое внимание на
оставшийся от источника задачи "город" :).
D. Половинное деление.
H. Военная сортировка.
I. Космический мусорщик.
A. День рожденья архимага
Максимальное
время работы на одном тесте:
|
1 секунда
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
Ковен магов планирует празднества по случаю дня рожденья архимага, но
архимаг уже настолько стар, что точную дату его дня рождения все забыли. В
архивах нашлись следующие возможные даты дня рождения архимага:
- 15 лым сылан, 16 лым сылан, 19 лым сылан;
- 17 эж петан, 18 эж петан;
- 14 лоддза-номъя, 16 лоддза-номъя;
- 14 нинпу, 15 нинпу, 17 нинпу.
Ник и его учитель Васа пытаются восстановить точную дату дня рождения
архимага. В доверительном разговоре архимаг сообщает Нику месяц, в котором он
родился, а своему другу (учителю Ника) – число.
После этого между Ником и Васой произошел следующий разговор.
- Я не знаю, когда день рождения архимага, но я знаю, что ты тоже этого не
знаешь, - заявил Ник.
- Я и не знал, когда у архимага день рождения, но теперь знаю, - ответил Васа.
- А теперь и я знаю, когда он родился, - сказал Ник.
ТАК КОГДА ЖЕ РОДИЛСЯ АРХИМАГ?
Ваша программа должна вывести одну строку – дату рождения архимага.
Формат входных данных
Нет входных данных.
Формат выходных данных
Одна строка – число и месяц.
B. Эльфийская свита дракона
Максимальное
время работы на одном тесте:
|
2 секунды
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
По дороге двигалась странная процессия. Странность ее была не в том, что
она состояла из отряда эльфов, а в том, что впереди отряда двигался самый
настоящий дракон. Дракон в основном двигался легким бегом, трудно представимым
для такого массивного тела. Иногда он радовал сопровождающих эльфов своими
знаменитыми прыжками, в результате чего им приходилось нагонять его галопом. Но
дракон оказался понятливым и подстраивался под среднюю скорость передвижения
процессии.
Рассматривается система двух объектов – отряд эльфов и дракон. Отряд эльфов
состоит из неизвестного количества пар всадник-конь. Скорости всех эльфийских
всадников известны и одинаковы (0 < u <= 1000000000). Скорость
дракона v также известна и больше скорости эльфов (u < v). Требуется
определить среднюю арифметическую скорость системы двух объектов.
Формат входных данных
Последовательность целых чисел: скорости эльфов и дракона.
Формат выходных данных
Действительное число.
Пример
C. Астральный архив
Максимальное
время работы на одном тесте:
|
2 секунды
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
Магия и программирование слились в инфомагию. Инфомаги как боги – создают
материальное, программируя его свойства. Захватывающе интересное занятие. Все
ли могут боги? Где границы возможностей инфомагов? Насколько этично создание
живого?
Эти и другие вопросы широко обсуждаются магами в астрале. Маги обмениваются
мыслеформами. Мыслеформа позволяет передавать не только содержание, но и
эмоциональную окраску. К сожалению, мыслеформа долго не хранится. Для записи
обсуждений был создан астральный архив, где мыслеформы кодируются в записи.
Структура архива проста: каждая запись либо начинает новую тему, либо является
ответом на какую-либо предыдущую запись и принадлежит той же теме.
Широкая общественность интересуется, какая тема наиболее популярна у магов.
К вам обратились с просьбой выяснить это.
Формат входных данных
Первая строка содержит целое число N– количество записей в
архиве (1 ≤ N ≤ 1000). Следующие строки содержат описание записей в хронологическом
порядке.
Описание записи, которая представляет собой начало новой темы, состоит из
трех строк. Первая строка содержит число 0. Вторая строка содержит название
темы. Длина названия не превышает 30 символов. Третья строка – текстовое
содержание записи.
Описание записи, которая является ответом на другую запись, состоит из двух
строк. Первая строка содержит целое число ‑ номер записи, ответом на которое
оно является. Записи нумеруются, начиная с единицы. Ответ всегда появляется
позже, чем запись, ответом на которую она является. Вторая строка содержит
текст записи. Гарантируется, что в текстовых строках только один символ начала
новой строки.
Длина всех текстовых записей не превышает 100 символов.
Формат выходных данных
Выведите название темы, к которой относится наибольшее количество записей.
Если таких тем несколько, то выведите первую в хронологическом порядке.
Пример
in
|
out
|
7
0
Что такое
хорошо?
Крошка сын
к отцу пришел, и спросила кроха:- Что такое хорошо и что такое плохо?
0
Что такое
плохо?
Если ветер
крыши рвет, если град загрохал,- это для прогулок плохо.
1
Солнце в
целом свете. Это - очень хорошо и большим и детям.
1
- Если
мальчик любит труд, тычет в книжку пальчик, про такого пишут тут: он
хороший мальчик.
2
От вороны
карапуз убежал, заохав. Мальчик этот просто трус. Это очень плохо.
4
Этот, хоть
и сам с вершок, спорит с грозной птицей. Храбрый мальчик, хорошо, в жизни
пригодится.
6
Мальчик
радостный пошел, и решила кроха: "Буду делать хорошо, и не буду -
плохо".
|
Что такое хорошо?
|
D. Платье для Золушки
Максимальное
время работы на одном тесте:
|
2 секунды
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
Ник приглашен на бал к архимагу. Крис, амбициозная студентка академии
магии, ‑ достойная спутница для статусной вечеринки, но у нее нет
соответствующего случаю платья. Для инфомага это не проблема – платье можно
создать! Прежде всего, создается информационная структура ткани – узлы,
соединенные связями. Итак, имеется N узлов, описывающих
будущее платье. Некоторые из узлов соединены связью. Связь овеществляется,
причем, очевидно, для любых двух соединенных связью узлов A и B овеществление
можно произвести ровно один раз.
Прочность ткани зависит от взаимной удаленности узлов. Назовем взаимной
удаленностью друг от друга трех узлов A, B и C минимальное количество связей,
которое необходимо использовать, чтобы «пройти» от A до B, затем от B до C и
затем от C до A (при этом разрешается использовать одну и ту же связь в
различных обходах). Маг хочет найти три узла в структуре ткани, для которых
взаимная удаленность друг от друга будет максимальной.
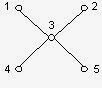
Например, для пяти узлов, соединенных так, как это показано на рисунке 1,
три наиболее удаленных друг от друга узла ‑ это узлы 1, 2 и 5
(взаимная удаленность равна 2 + 3 + 3 = 8). А для
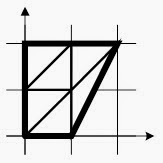
узлов на рисунке 2 – это любые три узла, выбранные из
множества {1, 2, 4, 5} (удаленность 2 + 2 + 2 = 6).
Рисунок 1. Решение 1, 2, 5.
Рисунок 2. Решение неоднозначно.
Формат входных данных
Первая строка содержит число N – количество узлов (3 ≤ N ≤
1000). Следующие N строк содержат описания узлов. Описание i-го
узла сначала содержит Ki – количество узлов, с которыми он соединен
связями (1 ≤ Ki < N), а затем Ki чисел
– номера узлов, с которыми он соединен.
Гарантируется, что входные данные корректны, то есть, если есть связь
узла A с узлом B, то есть и связь B с A, причем для всех пар узлов выполняется
свойство, указанное в условии задачи.
Формат выходных данных
Выведите три различных числа – номера трех наиболее удаленных друг от друга
узла в произвольном порядке. Если решений несколько, выведите любое из них.
Примеры
in
|
out
|
5
1 3
1 3
3 1 2 4
2 3 5
1 4
|
1 2 5
|
5
1 3
1 3
4 1 2 4 5
1 3
1 3
|
1 2 4
|
E. Броня из ткани
Максимальное
время работы на одном тесте:
|
2 секунды
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
Платье Крис на балу у архимага произвело фурор, и маги
бросились придумывать новые способы создания ткани и областей использования
новой технологии. Тем более, что их энтузиазм подогревался невестами и женами J.
Нашлись и теоретики, заметившие, что особо прочная ткань для защитного доспеха
будет получаться, если каждую деталь будущего доспеха можно разбить на
треугольники равной площади. Упрощая модель, будем считать, что каждую деталь
доспеха можно представить выпуклым плоским многоугольником, вершины которого
лежат в точках с целочисленными координатами. Требуется разбить его на
треугольники с вершинами в точках с целыми координатами, каждый из которых имел
бы площадь ½, либо выяснить, что это сделать невозможно.
Рисунок 1. Разбиение многоугольника на треугольники с площадью ½.
Формат входных данных
Первая строка содержит число N – количество вершин
многоугольника (1 ≤ N ≤ 10). Следующие N строк содержат
координаты вершин многоугольника в порядке обхода их по часовой стрелке. Все
координаты – целые неотрицательные числа, не превышающие 10. Никакие три
последовательные вершины многоугольника не лежат на одной прямой.
Формат выходных данных
Если выполнить разбиение указанным образом невозможно, выведите в выходной
файл единственное число 0.
В противном случае выведите несколько строк, содержащих по 6 чисел каждая.
Количество строк должно быть равно количеству треугольников в найденном
разбиении. Числа в каждой строке должны представлять собой координаты вершин
соответствующего треугольника x1, y1, x2, y2, x3, y3.
Площадь каждого треугольника должна быть ½. Порядок перечисления треугольников
и вершин в каждом из треугольников может быть произвольным. Если допустимых
разбиений несколько, выведите любое.
Пример
in
|
out
|
4
0 0
0 2
2 2
1 0
|
0 0 1 1 1 0
0 0 1 1 0 1
0 1 1 1 1 2
0 1 1 2 0 2
1 0 2 2 1 1
1 1 2 2 1 2
|
F. Оловянные солдатики
Максимальное
время работы на одном тесте:
|
2 секунды
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
Проблема искусственного интеллекта в целом решена. Но, как всегда, решение
одной проблемы ведет к появлению десятка новых. Одна из таких новых проблем –
воспитание молодых магов, развитие их собственного интеллекта, достаточного для
управления Искином. Проблему пытаются частично решить созданием обучающих игр.
Вот детская игрушка-головоломка для самых маленьких – набор из N оловянных
солдатиков, управляемых «коллективным разумом». У каждого солдатика есть
идентификационный номер – число в диапазоне от 1 до N. Каждый
солдатик может выполнять простейшие действия, которые не надо специально
программировать. Например, два солдатика могут обменяться местами, получив
соответствующий приказ от «коллективного разума».
В начале игры все солдатики выстраиваются в ряд так, что ни один солдатик
не стоит на своем месте, то есть его идентификационный номер не равен номеру
занимаемой им позиции. Ребенку-магу требуется создать программу перестановок
солдатиков для Искина, учитывая, что меняться местами могут только рядом стоящие
солдатики. При этом, если какой-то солдатик занял свое место, то он уже не
может сдвинуться с него. Например, пусть в наборе из 6 солдатиков в некоторый
момент солдатики расположились в порядке [2, 1, 3, 6, 4, 5]. Тогда можно поменять местами 1 и 2, 6
и 4 или 4 и 5 солдатика, а менять местами 1 и 3, или 3 и 6 нельзя, поскольку
солдатик 3 находится на своем месте (на позиции с номером 3).
Обычно малыши довольно легко справляются с программированием «коллективного
разума», управляющего солдатиками. А справитесь ли вы? Вам дан входной массив,
в котором ни один солдатик не стоит на своем месте. Найдите последовательность
обменов (не обязательно кратчайшую), переставляющую солдатиков и
удовлетворяющую приведенным условиям.
Подсказка. Найти такую последовательность
обменов всегда возможно.
Формат входных данных
Первая строка содержит целое число N – размер входного
массива (1 ≤ N ≤ 100). Вторая строка содержит N целых чисел – исходную
перестановку чисел от 1 до N в массиве. Изначально ни одно число не стоит на
своем месте.
Формат выходных данных
Выведите K строк, где K– количество обменов в
Вашей сортировке. На каждой строке выведите по два числа xi и yi,
разделенных пробелом – позиции в массиве, числа на которых следует поменять
местами на i-ом обмене. Помните, что должно выполняться условие и что нельзя перемещать число, которое уже стоит на своем месте.
Пример
in
|
out
|
6
2 3 1 6 4 5
|
2 3
1 2
4 5
5 6
|
В приведенном примере массив последовательно имеет следующий вид:
исходный
ряд солдатиков
|
2 3 1 6 4 5
|
поменяли
местами солдатиков на 2 и 3 позициях
|
2 1 3 6 4 5
|
поменяли
местами солдатиков на 1 и 2 позициях
|
1 2 3 6 4 5
|
поменяли
местами солдатиков на 4 и 5 позициях
|
1 2 3 4 6 5
|
поменяли
местами солдатиков на 5 и 6 позициях
|
1 2 3 4 5 6
|
G. Пространственное кружево
Максимальное
время работы на одном тесте:
|
2 секунды
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
Создание украшений было и остается любимым занятием магов-гномов. Типовая
технология предполагает создание информструктуры в некоторой трехмерной области
пространства заданием трехмерной сетки будущего украшения и затем ее
«овеществление». Однако недавно появился новый прием. Он состоит в плетении
«кружева». Предполагается, что новый прием заметно повысит производительность
труда.
Инструментом является некоторый объект (назовем его паук), который может
передвигаться в пространстве по 6 направлениям: на север (N), на юг (S), на запад (W),
на восток (E), вверх (U) и вниз (D). Перемещаясь, паук формирует
информструктуру. Движением паука управляет Искин. Программа движения задается
шестью правилами движения, которые соответствуют каждому из указанных
направлений. Каждое такое правило представляет собой строку символов из
множества {N, S, W, E, U, D}.
Команда паука есть пара из символа направления и параметра целого
положительного числа M. При исполнении такой команды паук в
соответствии со своей программой выполняет следующее. Если параметр больше 1,
то он перемещается на один шаг в направлении, которое указано в команде, а
затем последовательно выполняет команды, заданные правилом для данного
направления, с параметром меньше на 1. Если же параметр равен 1, то просто
перемещается на один шаг в указанном направлении.
Пусть, например, заданы следующие правила:
Направление
|
Правило
|
N
|
N
|
S
|
NUSDDUSE
|
W
|
UEWWD
|
E
|
|
U
|
U
|
D
|
WED
|
Тогда при выполнении команды S(3) паук
выполнит следующие действия:
1. переместится
на 1 шаг в направлении S;
2. выполнит
последовательно команды N(2), U(2), S(2), D(2), D(2), U(2), S(2), E(2).
Если далее проанализировать действия паука
при выполнении команд из пункта 2, получим, что в целом он совершит следующие
перемещения: SNNUUSNUSDDUSEDWEDDWEDUUSNUSDDUSEE
По заданной команде определите, какое общее количество перемещений на один
шаг совершит паук при выполнении заданной команды. В приведенном примере это
количество равно 34.
Формат входных данных
Первые шесть строк задают правила для команд с направлением N, S, W, E, U и
D соответственно. Каждая строка содержит не более 100 символов (и может быть
пустой). Следующая строка содержит команду ловушки: сначала символ из множества
{N, S, W, E, U, D}, затем пробел и параметр команды – целое положительное число, не
превышающее 100.
Формат выходных данных
Выведите единственное число ‑ количество перемещений, которое совершит
паук. Гарантируется, что ответ не превышает 109.
Пример
in
|
out
|
N
NUSDDUSE
UEWWD
U
WED
S 3
|
34
|
H. Магическая защита
Максимальное
время работы на одном тесте:
|
1 секунда
|
Максимальный
объем доступной памяти:
|
8 мегабайт
|
Магическая защита обычно строится как полусфера, нижняя часть которой
представляет собой окружность. В отдельных точках этой окружности маг может
размещать дополнительные заклинания для защиты и нападения. Маги называют такие
точки реперами. Теоретически количество заклинаний зависит от количества
реперов N. На практике, сильный инфомаг может разместить столько заклинаний, сколько
существует незамкнутых ломаных, соединяющих реперы. Каждая такая ломаная состоит
из N - 1 хорды. Единственное условие, такие ломаные не должны иметь
самопересечений.
Ник проектирует свою защиту. Сколько заклинаний он сможет разместить, если
возьмет N реперов.
Формат входных данных
Одно
целое число N (3 ≤ N ≤ 30).
Формат выходных данных
Одно целое число – количество заклинаний.
Пример