A. Ворота в школу
В школу Мерлина в Кармартéне
принимали всякого, кто сумел найти ее, войти в нее, разыскать там профессора
Мерлина и ответить ему по билету. В день, когда Гвидион вошел в городские
ворота, отыскал школу на рыночной площади и постучался у ее дверей, Мерлин был
в отлучке.
Как видно из рисунка, ворота в школу двустворчатые,
симметричные и невидимые. Ну и что, что вы их видите. А обычные люди вместо
ворот видят каменную кладку. Впрочем, членам городского магистрата и другим
персонам, например членам инспектирующей комиссии Министерства образования,
вручались амулеты, позволяющие увидеть скрытые иллюзией ворота. Для расчета требуемой
мощности амулета долгое время использовалась простейшая формула площади
прямоугольника, полностью содержавшего ворота, но в условиях кризиса было
решено оптимизировать мощность амулетов, тем более что их нужно все больше и
больше.
Точным решением задачи для одной створки ворот является вычисление
интеграла
где подынтегральная функция
описывает верхнюю кромку ворот, а пределы интегрирования позволяют определить
ширину створки ворот. На рисунке справа показано, что значение определенного
интеграла равно площади фигуры, ограниченной тремя прямыми и линией y = f(x). Пифагор, преподававший в школе
математику, предложил заменить неизвестную функцию линейной: f(x) = kx + c. Гвидион и Леввелис были отправлены к воротам, производить
замеры. От вас требуется написать программу вычисления площади ворот по
полученным размерам.
Формат
входного файла
Одна
строка содержит три действительных числа: w = (b – a) – ширина одной створки ворот, h – наименьшая высота ворот и H – наибольшая высота ворот (в центре).
Формат
выходного файла
Одно
действительное число – площадь ворот ровно с двумя цифрами
в дробной части.
Пример
input
|
output
|
1.5
2.1 3.9
|
9.00
|
Решение
Решение задачи очевидно. Створка ворот - прямоугольная трапеция. Площадь двух одинаковых примоугольных трапеций равна (h + H)*w.
B. Поэзия Туата Де
Дананн
На самом первом уроке поэзии Туата Де
Дананн Мак Кархи, напомнив в двух словах о том, кто такие Туата Де Дананн,
прочел вслух несколько фрагментов поэм. Возникали и рушились замки, облетал
жасмин, проносились стада оленей, садилось солнце, засыпали дрозды в тисовых
рощах. Бервин разинул рот так, что туда мог бы залететь жаворонок.
- Сосредоточьтесь,
пожалуйста, Бервин, в этом слове два слога, первый долгий, второй ударный, -
безмятежно говорил Мак Кархи.
Для восстановления темных мест в поэзии Туата Де Дананн четвертого века используется следующий прием. Берется
сохранившаяся строфа и записывается с использованием обозначений ударных и
долгих слогов. Полагают 1 – ударный слог, 0 – долгий слог. Например, слоговая
запись строфы 28 в перечне строф выглядит как 11100. Одна из наиболее известных
и простых модификаций сводится к тому, чтобы получить строфу с четным
количеством ударных слогов, заканчивающуюся долгим слогом. То есть
подсчитывается количество ударных слогов в слоговой записи строфы и дописывается
справа 1, если это количество нечетно, или 0, если количество ударных слогов
четно. После этого дописывается 0.
Например, в записи 11100 количество ударных слогов нечетно,
поэтому добавляем справа еще одну 1. Получили 111001. Дописываем нуль, получаем
1110010. В перечень строф эта модификация включается под номером 114. Перечень
строф непустой и набольший номер в нем меньше 2000000000.
Молодой преподаватель школы Мак Кархи, ученик Мерлина,
поручил Бервину, сыну Эйлонви, седьмому сыну мельника из-под Кардиффа, для
строфы, построенной с помощью указанной модификации, имеющей номер строго
больше R, найти номер исходной строфы из перечня.
Вам поручается составить программу для решения этой задачи.
Формат входного файла
Первая строка содержит одно целое число R (1 <= R < 2000000000).
Формат выходного
файла
Одно число – минимальный номер строфы, после модификации
которой указанным способом получается строфа с номером большим R.
Пример
Решение
Задача по мотивам ЕГЭ по информатике. Для модификации надо установить бит четности (количество 1 станет четным) и удвоить число. Решаем обратную задачу: перебираем четные числа строго большие R, пока не найдем число с четным количеством единиц. Уменьшаем его в 4 раза.
Вот мое решение:
int
one(unsigned long n)
{
//подсчет количества единиц в двоичном представлении
int i= 1;
while (n &= n-1) {
i++;
}
return i;
}
int main(int
argc, char* argv[])
{
unsigned long b;
scanf("%u",&b);
//кандидатами
на искомое число будут четные числа, большие b
if (b%2
!= 0) {b++;} else b += 2;
//Начинаем
перебор.
while(one(b)
% 2) { /* У каждого кандидата
проверяем
четность количества 1 в двоичном представлении. */
b
+= 2;
}
/*
Когда такое будет найдено, убираем два последних бита.
Это
и есть искомое N. */
printf ("%u\n",
b>>2);
system ("pause");
return 0;}
Красивое решение было у команды - победительницы. Предлагайте в комментариях свои решения.
C. Классики и
эпигоны
- Вы знаете, в чем
отличие поэзии Семерых мудрецов бамбуковой рощи от поэзии Ли Бо и его
современников? - говорил Сюань-цзан.
- Да? - медлительно
отзывался Финтан, склонившись над доской.
- Ли Бо - настоящий
классик. Вот вам пример. Можно себе представить, что Ли Бо почему-либо вдруг
поставили где-нибудь памятник. Это странно, согласен, но это можно себе
представить. А вот если попытаться поставить памятник кому-нибудь из Семерых
мудрецов бамбуковой рощи, этот памятник непременно или сделает неприличный жест
и убежит, или еще как-нибудь себя проявит, - к примеру, растает в воздухе.
- Да, понимаю, - говорил
Финтан. - То же и в нашей поэзии: со временем все вырождается в классику.
Китайская классическая теория заклинаний обычно использует наборы
слов, в которых ни одно слово из набора не является началом другого слова. В
европейской традиции о таких наборах говорят, что они удовлетворяют условию Fano, Например, набор слов
“abra”, “cada”, “bra” – удовлетворяет условию Fano, а набор “a”, “bra”,”cad”, “abra”
– нет, поскольку слово “a”
является началом слова “abra”.
Профессор Сюань-цзан назвал такие наборы беспрефиксными,
строго определив понятие префикса: слово A называется префиксом слова B, если A
получается из B
удалением нуля или более букв в конце. Например, слова “”, “a”, “ab”, “aba”
являются префиксами слова “aba”.
Развивая труды древних, профессор ввел понятие почти беспрефиксных наборов слов.
Определение. Набор
слов называется почти беспрефиксным уровня k, если наибольший общий префикс двух любых слов из набора не
превышает по длине k.
Например, “abac”,
“abc”, “ba” является почти
беспрефиксным набором уровня 2, а набор “abac”, “abab”,
“ba” – нет, поскольку
наибольший общий префикс слов “abac”
и “abab” имеет длину 3.
Профессор хочет удостовериться, что идея почти беспрефиксных кодов
содержательна, и проверить, какие наборы получаются над классическим и
современными списками «волшебных» слов.
Проводить численные эксперименты придется ученику
профессора, милому и улыбчивому Афарви, сыну Кентигерна. Напишите для него
программу, которая по заданному набору слов и числу k выберет из заданного списка слов
максимальный набор, который является почти беспрефиксным набором уровня k.
Формат входного файла
Первая строка содержит два целых числа: n и k – количество слов в списке и уровень почти беспрефиксного набора,
который требуется построить (1 <= n <= 100000, 0<= k <= 200). Следующие n строк содержат список слов
(по одному слову в строке). Слова состоят из строчных букв латинского алфавита.
Длина каждого слова от 1 до 200 букв. Суммарная длина всех слов не превышает
миллион букв. Все слова различны.
Формат выходного
файла
В первой строке одно число – максимальное количество слов,
которые можно выбрать из данного списка, чтобы они образовывали почти
беспрефиксный набор уровня k. Следующие строки содержат сам этот набор – по
одному слову в строке.
Пример
input
|
output
|
6 2
aba
bacaba
abacaba
baca
abac
caba
|
3
aba
bacaba
caba
|
Решение
Эта и следующие две задачи взяты из архива IX Всероссийской командной олимпиады школьников по программированию 2008-209 года. Соответственно
С. Почти беспрефиксные коды
D. Обход в глубину
H. Шкафы
В материалах есть презентация с решением задач, тесты и решения жюри.
D. Перемещение по школе
Здание
школы, украшенное многими башнями, переходами, воздушными арками и подвесными
мостами, делилось на три части, которые назывались четвертями, - Южную,
Северную и Западную.
Проискав все утро одинаковые носки,
Ллевелис, чтобы все-таки попасть на древнегреческий, решил срезать дорогу. Ему
нужно было в Винную башню, но вместо того, чтобы пройти поверху, не спуская с
этой башни глаз, он углубился в каменные переходы, которые, как ему показалось,
могут привести в Южную четверть скорее. В месте раздвоения лестницы Ллевелис
рискнул пойти направо и вышел в двусветный зал, где ему вдруг показалось, что
он в какой-то забытой части школы, куда никто никогда не придет. Он ужаснулся и
очертя голову кинулся вниз по истертым ступеням в ближайшую арку. С разбегу он
вылетел к подножию барельефа с пляшущим драконом. "Тут, кажется, на этом барельефе
надо что-то нажать, он провернется, и за ним откроется какой-то коридор... или
вход в поточную аудиторию, не помню", - и Ллевелис запрыгал на месте,
пытаясь достать повыше и стукнуть кулаком по нужному месту барельефа. …Тут
Ллевелис внезапно понял, что с ним случилось. Он забрел в башню Бранвен, и,
пока он бегал внутри нее, она плавной походкой переместилась из Южной четверти
в Северную.
Как вы, надеюсь, поняли из длинного вступления, попасть в
нужное место ученикам школы часто бывает непросто. Мало того, что меняет свое
положение башня Бравен, так еще и профессора школы перемещают двери, строят или
убирают арки и даже устанавливают новые места для занятий.
К счастью, школа сама следит за изменениями, строя граф. Вершины
графа суть башни и прочие значимые места, а ребра – коридоры, лестницы, арки, мостики
и двери. Для контроля доступности всех помещений школа выполняет обход графа в
глубину и хранит его результат. Ниже представлена программа, которой пользуется
школа, для вашего удобства на двух популярных языках.
Паскаль
|
Си
|
var
a : array [ 1 . . maxn , 1 . .
maxn ] of boolean ;
v i s i t e d : array [ 1 . . maxn ] of boolean ;
procedure d f s ( v : integer ) ;
var
i : integer ;
begin
writeln ( v ) ;
v i s i t e d [ v ] := true ;
for i := 1 to n do begin
if a [ v ] [ i ] and not v i s i t e
d [ i ] then
begin
d f s ( i ) ;
writeln ( v ) ;
end ;
end ;
end ;
procedure graph_dfs ;
var
i : integer ;
begin
for i := 1 to n do
i f not v i s i t e d [ i ] then d f s ( i ) ;
end ;
|
int a [ maxn + 1 ] [ maxn + 1 ] ;
int v i s i t e d [ maxn + 1 ] ;
void d f s ( int v ) {
p r i n t f ( "%d\n" ,
v ) ;
v i s i t e d [ v ] = 1 ;
for ( int i =
1 ; i <= n ; i++) {
i f ( ( a [ v ] [ i ] != 0) &&
( v i s i t e d [ i ]
== 0)) {
d f s ( i ) ;
p r i n t f (
"%d\n" , v ) ;
}
}
}
void graph_dfs ( ) {
for ( int i =
1 ; i <= n ; i++) {
if ( v i s i t e d [ i ] == 0) {
d f s ( i ) ;
}
}
}
|
В программе граф хранится в матрице смежности в массиве a, вершины графа
пронумерованы от 1 до n.
В массиве visited
помечается, какие вершины были посещены в процессе обхода.
Мерлин, глава школы, в помощь учащимся сообразил на коленке
артефакт, который дает доступ к записям школы, и, разумеется, через 5 минут
забыл, как он это сделал, или сказал что забыл, чтоб студенты думать не
разучились. Теперь студентам надо срочно восстановить граф, чтобы попасть на
урок, пока все пути опять не перекосило.
Формат входного файла
Первая строка содержит два целых числа: n и l – количество вершин в графе и количество чисел в выведенной
последовательности (1<= n
<= 300, 1 <= l
<= 2n-1). Следующие l строк по одному числу – вывод
программы. Гарантируется, что хотя бы один граф, дающий такой вывод, существует.
Формат выходного
файла
В первой строке одно
число m – максимальное
возможное количество ребер в графе. Следующие m строк содержат по два целых числа –
номера вершин, соединенных ребрами. В графе не должно быть петель и кратных
ребер.
Пример
input
|
output
|
6 10
1
2
3
2
4
2
1
5
6
5
|
6
1 2
1 3
1 4
2 3
2 4
5 6
|
Решение
Эта и следующая задача взяты из архива IX Всероссийской командной олимпиады школьников по программированию 2008-209 года. Соответственно
D. Обход в глубину
H. Шкафы
В материалах есть презентация с решением задач, тесты и решения жюри.
E. Шкаф-стеллаж
В пятницу Тарквиний
Змейк впервые допустил первый курс в химическую лабораторию, и первый день в
лаборатории Змейка запомнился всем надолго и многим - навсегда. Он привел их к
порогу этого храма, отпер дверь ключом и ушел, потому что его позвали. Все
сначала замерли на пороге, опасаясь сильно продвигаться вперед. Наконец, кто
посмелее, шагнул внутрь, а вслед за ними зашли и остальные и застыли,
рассматривая иронично глядящие на них портреты Мухаммеда ар-Рази и Альберта
Великого, а также порошки и жидкости, стоящие повсюду в шкафах и на полках.
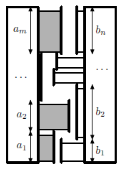
Два стоящие друг против друга лабораторных шкафа с
выдвижными ящиками для хранения реактивов привлекли особое внимание первокурсников: они стояли в узкой нише лицевыми сторонами друг к другу так, что выдвинуть одновременно два ящика, находящиеся напротив друг друга, было невозможно. Каждый шкаф имел несколько ящиков различной высоты. При просмотре снизу-вверх ящики в первом шкафу имеют высоту
a1, a2, …, am,
а ящики во втором шкафу b1,
b2, …, bn. Доступ к содержимому
ящиков осуществлялся с боковой стенки!
Первокурсники не знали, что для того, чтобы в течение
рабочего дня было одновременно открыто наибольшее количество ящиков, пришлось
провести вычисления с использованием немалых ресурсов Школы.
Повторите подвиг Тарквиния Змея, написавшего программу,
максимизирующую количество одновременно открытых ящиков и определяющую номера
этих ящиков.
Формат входного файла
Первая строка содержит два целых числа: m и n – количество ящиков в первом и во втором шкафу соответственно (1
<= m, n <= 100000). Вторая
строка содержит m целых
чисел a1, a2, …, am – высоты ящиков в первом шкафу.
Третья строка содержит n
целых чисел b1, b2, …, bn – высоты
ящиков во втором шкафу. Высоты ящиков положительные и не превосходят
1000000000.
Формат входного файла
Первая строка содержит два целых числа: k и l – количество ящиков, которые следует использовать в первом и во
втором шкафу соответственно. Сумму k + l следует максимизировать. Вторая строка содержит k целых чисел – номера ящиков
в первом шкафу, которые следует использовать. Третья строка содержит l целых чисел – номера ящиков
во втором шкафу, которые следует использовать. Если оптимальных решений
несколько, выведите любое.
Пример
input
|
output
|
5 5
1 2 3 4 5
6 4 3 2 1
|
3 4
1 2 3
2 3 4 5
|
Решение
Эта задача взята из архива IX Всероссийской командной олимпиады школьников по программированию 2008-209 года. Соответственно
H. Шкафы
В материалах есть презентация с решением задач, тесты и решения жюри.
F. Спальные носки
Профессор Лютгарда, дочь Рунхильды, дочери Гренделя, в холодные зимние
ночи, особенно если не хватало дров для камина, одалживала студентам свои
запасные шерстяные носки, в которых хорошо было спать как в спальном мешке.
Студенты говорили при этом, укладываясь в носок: "А вообще-то наша
Лютгарда очень изящная. И нога у нее маленькая. Вдвоем в ее носок никак не
втиснешься".
В сундуке Лютгарды хранятся прекрасные носки из исландской
шерсти, из шерсти альпаки, верблюда, ангорских коз, все они украшены разнообразными
орнаментами, теплые, пушистые, с искусно вывязанной пяткой. Всего в сундуке n
разных сортов носков. Два друга, Гвидион и Ллевелис, задумали обеспечить
всех своих друзей (и себя конечно!) одинаковыми спальными носками. Но доброта и
терпение Лютгарды не бесконечны, поэтому вам предстоит выяснить, какое
минимальное количество носков друзьям надо достать из сундука, чтобы
гарантированно k носков оказались одинаковыми.
Формат входного файла
В строке через пробел записаны целые числа n≥1, k≥2.
Формат выходного файла
Одно целое число - минимальное количество носков.
Пример
Решение
Решение достигается путем недолгих размышлений. Потребуется n(k - 1) + 1 носков.
