Задачи XX открытого чемпионата СГУ по программированию
На чемпионате были предложены задачи, придуманные Езовских В.Е. для самых первых чемпионатов. Условия задач были на английском языке. Разбор задач от Котелиной Н.О.
Задача A. Bobby The Judge
Once Bobby heard that the lawyers' wages are enormous. So he decided to become a judge. The only problem is to pass an exam. The task at the examination is as follows. One has to sentence N (2≤ N≤32) criminals. The criminal number i (1≤ i≤ N) may be jailed for the period just from Si to Ei years (1≤ Si≤ Ei ≤ 1024). Is it possible to sentence each criminal so, that he will rest in the jail for Pi years under the condition – all Pi differ? Help Bobby, please! All numbers are integers.
Разбор
Дан набор из N отрезков на прямой. Требуется выяснить, можно ли выбрать N различных точек, чтобы в каждый отрезок попала хотя бы одна.
Можно использовать следующий жадный алгоритм. Отсортируем отрезки в лексикографическом порядке. Переберем отрезки. Будем для каждого отрезка выбирать наименьшую точку, лежащую на этом отрезке, которая еще не выбрана для предыдущих отрезков (для первого - это начало отрезка). Если такой точки для некоторого отрезка нет, ответ IMPOSSIBLE.
Если для всех отрезков точки найдутся, ответ POSSIBLE.
Задача B. The Puzzle for Aliens
Many years ago there were N (3≤ N≤ 1024) villages on the Earth surface. Aliens had defined geographical coordinates (the latitude Ti and the longitude Gi) of each village. The devices of aliens were rather poor and the coordinates were measured with the accuracy equal to a degree. So, Ti is an integer (0≤ Ti≤ 90) and Gi is an integer (0≤ Gi≤ 180). The numerical values are followed by the letters S (southern latitude), N (northern latitude), W (western longitude), E (eastern longitude). Aliens had to define the shortest distance between villages (the distance is measured on the Earth surface). They were solving this problem for a long time, but – no success! So they spat a little and had flied to their native planet. Are you able to solve this problem? You may suppose that the Earth has the form of the sphere with the radius 6366 kilometers, the answer should be rounded to a kilometer.
Разбор
В задаче надо было найти минимальную длину дуги между парами точек на сфере. Чтобы решить задачу B, можно было перевести координаты из широты и долготы в декартовы, а затем вычислить углы между получившимися радиус-векторами точек, например при помощи скалярного произведения. Длина дуги соответствующей данному углу alpha тогда равна alpha*r.
Задача C. The Gadfly and The Windows
Bobby had installed the so-called "ОКНА СОК" and just as a result his beloved gadfly OVOD has some problems. Every time OVOD goes inside by the shortest way. But those multi-layer windows! Each window consists of N (2≤ N ≤ 16) layers at the fixed distance (an inch). Each layer is just a checked square (four times four, side of the check is equal to an inch) and only one of the checks is the layer pane (OVOD may bypass the layer only through the pane). Look at the picture just below – this is an example of the layer
OVOD may penetrate only through the green square. Such a layer may be defined by a single integer (the left-upper corner – zero, the green square above – just six). For a better understanding the picture just below demonstrates OVOD flight through two-layer window
The OVOD's way is marked with red and its length is equal to
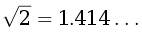. You are to find the length of OVOD's flight inside the window with the accuracy two digits after the decimal point.
Разбор
Надо найти длину пути овода. Задачу можно решить методом динамического программирования: на каждом слое длина кратчайшего пути каждой из вершин квадрата форточки получается как минимум из длин кратчайшего пути для предыдущего слоя для четырех вершин квадрата форточки плюс расстояние между соответствующими точками. В конце нужно взять минимум из 4 значений кратчайшего пути для вершин квадрата n-ой форточки.
Задача D. The Two's Powers
Just as everybody knows, Bobby likes the powers of two. So once he calculated all powers of two up to N (2≤ N ≤ 20) and has tried to settle those numbers in such an order that the total result of concatenation would be maximal. For example, if one takes N=5, then powers of two will be 1, 2, 4, 8, 16, 32 and the result will be 84322161. Are you able to gain the result for a given number?Разбор
Здесь надо было вычислить все степени двойки до N и написать их в таком порядке чтобы получившееся число было максимальным. Чтобы решить эту задачу, можно было отсортировать массив строк, соответствующих степеням 2, используя тот факт что строка a должна предшествовать строке b в массиве если строка a + b лексикографически больше чем строка b + a. Затем вывести получившиеся строки
Задача E. The Frequencies
Once Bobby read that the irrational numbers, such as are the perfect mixture of digits. So one can find any decimal digit as many times as he wants. Bobby likes the powers of two, so he decided to find the minimal power of two in which the predefined decimal digit from 0 to 9 encounters some times (from 1 to 9). For example, minimal power of two where six encounters twice is sixteen (216=65536). Help Bobby, please!Разбор
Нужно вычислять степени двойки до тех пор пока число вхождений заданной цифры не будет больше или равно заданного количества.
Задача F. The Digits on The Clock
The digital clock is on the Bobby's TV set. It shows hours, minutes and seconds, so during a day it runs from 00:00:00 to 23:59:59. Bobby tried to calculate the sum of those numbers (omitted colons) but failed. Are you able to define this sum?
Разбор
В этой задаче надо просуммировать все числа от 0 до 235959, которые получаются удалением двоеточий из времен, заданных в формате hh:mm:ss
int main(){
//
long long sh = 0;
long long sm = 0;
long long ss = 0;
for (int h=0; h <=23; h++){
for (int m =0; <=59; m++){
for (int s = 0; <=59; s++){
x +=h*10000+m*100+s;
}
}
}
cout << x;
}
