Разбор задач квалификационного тура 2018

Четвертьфинал Чемпионата мира по программированию по Уральскому региону. Квалификационный тур, 6 октября 2018 года

Полные условия задач здесь: https://app.luminpdf.com/viewer/n5At4ni4YwXzRfHHf

Задача A. Дота-сатанисты

На английском языке специалистов, занимающихся машинным обучением, часто называют datascientists, на русском это звучит как дота-сатанисты. Самые безумные дота-сатанисты занимаются исследованием свежести яблок. Для проверки качества своего алгоритма машинного обучения дота-сатанист сначала вручную определяет для каждого яблока, является ли оно свежим. После этого дота-сатанист отдаёт исследуемые яблоки своему алгоритму, и тот высказывает своё мнение об их свежести. Для каждого яблока бывает четыре вида исходов:
1. Истинно положительный — яблоко было свежим, и алгоритм определил яблоко как свежее.
2. Истинно отрицательный — яблоко было испорченным, и алгоритм определил яблоко как испорченное.
3. Ложно положительный — яблоко было испорченным, а алгоритм определил яблоко как свежее.
4. Ложно отрицательный — яблоко было свежим, а алгоритм определил яблоко как испорченное.
Известно количество истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных исходов. Вам нужно посчитать процентное соотношение ложных исходов к общему числу исходов. Гарантируется, что у дота-сатаниста было хотя бы одно яблоко, а ответ на задачу всегда выражается целым числом процентов.

Разбор
Количество ложных исходов равно Fp + Fn
Количество всех исходов равно Tp + Tn + Fp + Fn
Соответственно, процентное соотношение ложных исходов к общему числу исходов
равно 100 * (Tp + Tn + Fp + Fn)/ ( Fp+Fn) 
Соответственно, для решения задачи достаточно вывести данную выше формулу.

Задача B. Статистические выбросы

Пусть у нас есть серия из n экспериментов, результатами которых являются целые числа x1, x2, . . . , xn. Также известны ожидаемый результат эксперимента и максимальное допустимое отклонение — целые числа m и s. Назовём результат эксперимента выбросом, если он отличается от ожидаемого результата серии более чем на максимальное допустимое отклонение. Найдите все выбросы в данной серии экспериментов.
Формат входных данных
В первой строке записано целое число m — ожидаемый результат эксперимента ( − 10^4 ⩽ m ⩽ 10^4). Во второй строке записано целое число s — максимальное допустимое отклонение (0 ⩽ s ⩽ 10^4). В третьей строке записано целое число n (1 ⩽ n ⩽ 100). В последующих n строках по одному в строке записаны n целых чисел — результаты экспериментов x i ( −10^4 ⩽ xi ⩽ 10^4).
Формат выходных данных
Выведите все выбросы по одному в строке, порядок вывода значения не имеет.

Разбор
Из условия задачи следует, что xi является выбросом, если выполняется условие |xi − m| > s. В данной задаче достаточно найти все выбросы линейным проходом по множеству всех результатов экспериментов, сразу же печатая их в поток вывода.

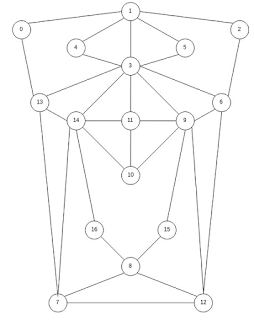
Задача C. Не отрывая карандаша

Наверняка вы не раз видели задачи, в которых нужно нарисовать рисунок, не отрывая карандаша от бумаги и не проводя по одной и той же линии более одного раза. Сейчас вам предстоит решить ещё одну такую задачу.

Формат входных данных

В данной задаче всего один тест, описывающий рисунок, приведённый в условии задачи. В первой строке теста через пробел записаны два целых числа — количество узлов и линий в рисунке.

В каждой из последующих 32-х строк через пробел записана пара целых чисел — номера узлов, соединённых линией.

Программа, которую вы напишете, может считать тест из входных данных и обработать его, или сразу выдать правильный ответ, не читая входные данные.

Формат выходных данных

В единственной строке через пробел выведите путь карандаша при рисовании данного рисунка в виде последовательности номеров узлов, в которых побывает карандаш. У этой задачи множество правильных решений, вы можете вывести любое из них.

Разбор

Данная задача является в точности задачей поиска Эйлерова пути в графе. Тут есть линейный алгоритм её решения. Также можно было написать экспоненциальный перебор всех обходов, либо подобрать ответ руками

Задача D. Расписание занятий

Вот так выглядит расписание звонков, которое вы можете найти рядом с деканатом матмеха:
1. 09:00 — 10:30
2. 10:40 — 12:10
3. 12:50 — 14:20
4. 14:30 — 16:00
5. 16:10 — 17:40
6. 17:50 — 19:20
7. 19:30 — 21:00
Дорога от дома до университета, как и дорога назад, занимает у Кирилла ровно 50 минут. После прихода из дома на первую пару в своём расписании Кирилл сидит в университете до конца последней пары в своём расписании, а потом едет назад домой. Посчитайте, сколько времени Кирилл суммарно потратит на то, чтобы съездить в университет, посетить там все пары и вернуться домой.
Формат входных данных
В единственной строке записаны два целых числа от 1 до 7 — номера первой и последней пар Кирилла. Номер первой пары не превосходит номера последней пары.
Формат выходных данных
Выведите время, потраченное Кириллом на поездку в университет, в формате hh:mm (часы и минуты через двоеточие).

Разбор
В данной задаче нужно вычесть из времени конца последней пары Кирилла время
начала первой и добавить к ответу 100 минут — суммарное время путешествия
Кирилла из дома в университет и назад. Все вычисления рекомендуется проводить в
минутах для простоты. Последней сложностью является соблюдение формата
вывода. Можно либо воспользоваться стандартными инструментами вашего языка,
либо написать форматирование руками.

Задача E. Многа Букафф

Успевай, пока все лучшее не расхватали! Выбирай стажировку сейчас, решай тестовое, проходи собеседование и получи приглашение на работу в крупной IT-компании. Предлагаем тебе за 2 месяца присмотреться к компании, примерить на себя роль разработчика, тестировщика или аналитика и принять решение о продолжении сотрудничества. У команды тоже будет время проверить твои знания, научить тебя и ввести в курс дела.
Стажировка в Контуре — это 2 месяца настоящей боевой практики в командах разработки. Студенты получают зарплату, все офисные плюшки, компенсацию питания и мощный комп за комфортным рабочим местом. А после удачного завершения стажировки — приглашение на постоянную работу.
Отбор на стажировку состоит из нескольких этапов. Первый: заполни заявку на сайте kontur.ru/intern. После этого ты получишь тестовое задание, на его выполнение у тебя будет месяц. Тех, кто отлично сделал тестовое, приглашаем на следующий этап — собеседование. Участники не из Екатеринбурга проходят его по скайпу. При положительном решении, через несколько недель ты получишь оффер на стажировку и можешь спокойно сдавать зачеты, экзамены, защищать курсовую и не тратить время на собеседования и тестовые задания.
Перед решением задачи этого года, посмотри прошлогоднее тестовое и эталонные решения, остальные примеры найдешь на страницах стажировки прошлых лет. Не забудь посмотреть список распространенных ошибок, чтобы не допустить их в своей работе. Совет от стажеров прошлых лет: не оставляйте все на последнюю неделю или даже ночь — сделать быстро и качественно не получится.
Отлично решить тестовое помогут онлайн-курсы от Контура на ulearn.me. Их специально разработали наши программисты, чтобы помочь студентам постичь основы программирования, чистого кода, тестирования и других направлений. Регистрируйся, решай, самосовершенствуйся — все курсы бесплатные.
Подготовишься к стажировке осенью, получишь приглашение весной ;)

Слово называется красивым, если оно состоит только из русских букв, не содержит букв «ь» и «ъ», а гласные в нём чередуются с согласными (в частности, это означает, что слово содержит по крайней мере одну гласную и одну согласную буквы). Например, «тех», «его» и «даже» — это красивые слова, а слова «кто», «ночь» и «и» красивыми не являются.
Прочитайте объявление, напечатанное выше курсивом, и посчитайте количество красивых слов в нём — это число и будет являться ответом на задачу. Каждое красивое слово следует учитывать в ответе столько раз, сколько оно встречается в тексте. Слово, разделённое дефисом при переносе строки, следует считать одним цельным словом. Не считая случая переноса, все символы в тексте, не являющиеся русскими буквами, следует считать разделителями с лов. Так «онлайн-курсы» — это два слова: «онлайн» и «курсы».
Формат входных данных
В данной задаче всего один тест, входные данные которого состоят из единственного слова «Test». Обрабатывать эти входные данные не нужно. Электронная версия текста объявления доступна в проверяющей системе.
Формат выходных данных
Выведите единственное целое число — количество красивых слов в объявлении.

Разбор
Возможным решением является аккуратный просмотр всех слов объявления и подсчёт
количества красивых. Также, можно скопировать электронную версию текста из
условия и написать скрипт, который делает это за вас.

Задача F. Битовая магия

Дан массив a длины n, состоящий из целых неотрицательных чисел. Требуется посчитать количество целых неотрицательных чисел x таких, что для всех 1 ⩽ i ⩽ n верно утверждение:
ai OR x = ai.
Операция OR для двух битов определяется следующим способом:
• 0 OR 0 = 0
• 0 OR 1 = 1
• 1 OR 0 = 1
• 1 OR 1 = 1
Для вычисления операции OR для двух целых неотрицательных чисел нужно представить оба числа в двоичной системе счисления и применить OR к каждой паре битов в числах для каждого разряда по отдельности (если числа имеют разную длину в двоичном представлении, предварительно меньшее из них нужно дополнить ведущими нулями до длины большего).
Например, 35 OR 5 = 39, поскольку 1000112 OR 0001012 = 1001112.
Формат входных данных
В первой строке записано целое число n (1 ⩽ n ⩽ 105). В следующей строке через пробел записаны n целых чисел — элементы массива a (0 ⩽ a i ⩽ 231 − 1).
Формат выходных данных
Выведите единственное целое число — ответ на задачу.

Разбор
Для начала, давайте по заданному числу a поймем, для каких чисел x верно, что a OR x = a . Поскольку после применения операции OR битовая запись числа a не должна поменяться, то единичные биты x должны составлять подмножество единичных битов a . Иными словами, должно соблюдаться равенство: a AND x = x , где AND — операция побитового “И”. Легко видеть, что из утверждений a AND x = x и b AND x = x следует, что:
x = x AND x = (a AND x) AND (b AND x) = (a AND b) AND x .
Соответственно, для всех чисел x , удовлетворяющих условию задачи должно соблюдаться:
(a1 AND a2 AND . . . AND an) AND x = x .
Иными словами, все подходящие числа x — это битовые подмножества числа:
t = (a1 AND a2 AND . . . AND an) .
Количество подмножеств данного множества M — это мощность его булеана P (M) , которая вычисляется по формуле: |P (M)| = 2^|M| . Получаем, что для решения данной задачи достаточно посчитать число t , посчитать количество единичных битов в нём, пусть это будет o, и выдать в качестве ответа число: 2^o .

Задача G. Плюс и минус

Вот так выглядит плюс, нарисованный попиксельно в квадрате 3 × 3:
010
111
010
Вот так выглядит минус, нарисованный попиксельно в квадрате 3 × 3:
000
111
000
На вход дана картинка из пикселей размера n × m. Гарантируется, что каждая четырёхсвязная область картинки, состоящая из единиц, является отмасштабированной (увеличенной по обеим координатам в одно и то же целое число раз) версией либо плюса, либо минуса. Посчитайте, сколько на картинке нарисовано плюсов, а сколько минусов.
Множество пикселей M называется четырёхсвязной областью, если для любых двух пикселей a, b ∈ M существует последовательность пикселей x 1 , x 2 , . . . , x k, такая что:
1. a = x 1, b = x k;
2. ∀i ∈ [1 ..k] : x i ∈ M;
3. ∀i ∈ [1..k − 1] : пиксели x i и x i +1 смежны по стороне.
Формат входных данных
В первой строке записаны два целых числа n и m (1 ⩽ n, m ⩽ 10^3). Далее следуют n строк длины m, состоящие из нулей и единиц.
Формат выходных данных
Выведите два целых числа, разделённые пробелом: количество плюсов и количество минусов, изображённых на картинке.

Разбор
Первым шагом для решения данной задачи является поиск всех четырёхсвязных областей картинки, состоящих из единиц. Это можно сделать, с помощью алгоритма поиска в ширину, храня метки посещённости для каждой клетки картинки. Теперь по множеству клеток в четырёхсвязной области нужно научиться определять тип фигуры. Это можно сделать по соотношению количества клеток в фигуре к квадрату её высоты — как для плюсов, так и для минусов это соотношение является постоянным.

Задача H. Камень-ножницы-бумага

Камень-ножницы-бумага — игра для двух игроков по следующим правилам. Каждый игрок независимо от другого выбирает себе один из трёх предметов — камень, ножницы или бумагу. Если оба игрока выбрали одинаковый предмет, то засчитывается ничья. Если один игрок выбирает бумагу, а другой ножницы, то побеждает выбравший ножницы. Если один игрок выбирает ножницы, а другой камень, то побеждает выбравший камень. Если один игрок выбирает камень, а другой бумагу, то побеждает выбравший бумагу.

Никита и Олег играют в камень-ножницы-бумагу по необычным правилам. Изначально у Никиты есть a1 камней, b1 ножниц и c1 листов бумаги, а у Олега a2 камней, b2 ножниц и c2 листов бумаги, a1 + b1 + c1 = a2 + b2 + c2 = S. Ребята играют серию из S раундов, и в каждом раунде оба игрока могут выбирать предметы только из тех, что у них имеются. Результат каждого раунда вычисляется по обычным правилам игры. После каждого раунда предметы, сыгранные в нём, выбрасываются. Поскольку у Олега есть связь с космосом, то он знает все ходы Никиты наперёд, какую бы стратегию тот ни выбрал. Ребята договорились, что Олег выигрывает серию, если во всех S раундах он не проиграет и при этом сможет одержать победу хотя бы в одном раунде. Зная, сколько каких предметов у каждого из ребят, определите, сможет ли Олег выиграть серию раундов, если оба игрока будут действовать оптимально.

Формат входных данных

В первой строке записаны три целых числа a1, b1 и c1. Во второй строке записаны три целых числа a2, b2 и c2. Гарантируется что a1 + b1 + c1 = a2 + b2 + c2, а также 0 ⩽ a1 + b1 + c1 ⩽ 10^9.

Формат выходных данных

Выведите « YES», если Олег может выиграть серию раундов при оптимальных действиях обоих игроков. В противном случае выведите « NO»

Разбор

Рассмотрим ситуацию, когда Олег ни разу не проигрывает серию матчей. Поскольку Олег знает все ходы Никиты, то он может заранее продумать, как он будет отвечать на каждый ход и он проиграет только в том случае, если у Никиты будет слишком много предметов какого-то конкретного типа. Если говорить более строго, то можно показать, что достаточный критерий того, что Олег ни разу не проиграет — это:

a2 + c2 ≥ a1 ,      b2 + c2 ≥ c1 ,      b2 + a2 ≥ b1 .

Соответственно, если это условие не выполняется, то Олег точно проиграл. В обратном случае нам остаётся проверить, что Олег может выиграть хотя бы одну игру. Для этого достаточно, чтобы он мог выиграть хотя бы одну партию. Для этого можно проверить, что он может выиграть хотя бы одну игру и при этом не проиграть не одной.

Поскольку Олег заведомо знает ход всей партии, он может выбрать, каким предметом он выиграет и распределить все остальные свои предметы так, чтобы не проиграть. Мы уже умеем проверять, умеет ли Олег выигрывать по заданным количествам предметов у обоих игроков, так что достаточно перебрать победный предмет Олега и рассчитать оставшуюся партию, убрав сыгранную пару предметов Олега с Никитой.

Задача I. 500-SAT

Дана булева формула в конъюнктивной нормальной форме, требуется найти и вывести любую подстановку переменных, обращающую формулу в истину. Гарантируется, что в каждой скобке находится ровно 500 попарно различных литералов.

Конъюнктивная нормальная форма — это представление булевой формулы в виде конъюнкции дизъюнкций литералов.

Конъюнкция — логическое «И».

Дизъюнкция — логическое «ИЛИ».

Литерал — переменная или её отрицание.

Формат входных данных

На вход дана одна строка длиной не более 10^6 символов в виде:

( xi1 | xi2| !xi3| . . .)&(! xi4| . . .)& . . .

Где ik — это номер используемой переменной (1 ⩽ ik ⩽ 10^6). Не гарантируется, что переменные в формуле пронумерованы подряд идущими числами.

| — обозначение для логического «ИЛИ».

& — обозначение для логического «И».

! — обозначение для логического «НЕ».

Формат выходных данных

Если ответа для данной формулы не существует, то в единственной строке выведите « OMG». Иначе для каждой переменной xi, использованной в формуле, выведите одну строку следующего вида:

• xi = true, если в искомой подстановке переменная xi должна принимать истинное значение;

• xi = false, если в искомой подстановке переменная xi должна принимать ложное значение.

Строки можно выводить в любом порядке. Если задача имеет несколько решений, можно вывести любое из них.

Разбор

Прежде всего, заметим, что если в какой-то скобке одна и та же переменная встречается вместе со своим отрицанием, то такая скобка нам неинтересна, так как значение выражения в данной скобке заведомо истинно. Таким образом далее мы будем рассматривать только скобки, в которых все переменные уникальны, а значит в каждой из таких содержится по 500 различных переменных. 

Первое решение заключается в том, чтобы назначить всем переменным случайные значения. Посчитаем, какова вероятность, что при случайном назначении одна любая скобка обратится в 0 — в скобке 500 переменных и все они должны принять “неправильное” значение, значит, вероятность такого события равна ( 1/2)^500 . 

Поскольку скобок уж точно меньше чем символов, то мы можем считать, что их не более чем 10^6. Вероятность того, что любая скобка обратится в ложь при случайном назначении переменных уж точно не превосходит суммы вероятностей того, что каждая скобка независимо от других обратится в ложь. Получаем, что при случайном назначении переменных вероятность провала не превосходит 10^6 • ( 1/2)^500 . Нас это вполне устраивает.

Второе решение заключается в том, чтобы аккуратно оценить число скобок. После оценки получается, что при таких ограничениях скобок будет не более 500 , так что каждой скобке можно назначить какую-нибудь переменную, находящуюся в ней и дать этой переменной значение, необходимое для обращения скобки в истину.

Задача J. Точки сочленения

Дан простой ориентированный ациклический граф, содержащий n вершин и m рёбер, все вершины которого достижимы из вершины с номером 1. Точкой сочленения в таком графе назовём любую вершину, такую что при её удалении появятся вершины, не достижимые из вершины с номером 1.

Найдите все точки сочленения данного графа.

Формат входных данных

В первой строке записаны два целых числа n и m (1 ⩽ n ⩽ 10^5; 0 ⩽ m ⩽ 2 • 10^5). В последующих m строках содержится описание всех рёбер в графе. Каждое ребро задаётся парой целых чисел — номером вершины, откуда ребро исходит, и номером вершины, куда оно идёт (вершины пронумерованы от 1 до n).

Формат выходных данных

В первой строке выведите количество точек сочленения в данном графе. Во второй строке выведите их номера в произвольном порядке.

Разбор

С одной стороны, точка сочленения — это в точности внутренняя вершина дерева доминаторов данного графа. Отсюда следует решение через построение дерева доминаторов и выписывание всех его внутренних вершин.

С другой стороны, давайте внимательнее изучим понятие точки сочленения. Рассмотрим некоторую вершину v . Как понять, что v является точкой сочленения? Рассмотрим все такие вершины u , что в графе есть ребро (v, u) , обозначим множество таких вершин, как M . Заметим, что если вершина v является точкой сочленения, то в M будет лежать хотя бы одна вершина, которая станет недостижимой из 1 после удаления v . Допустим, что к вершине u ∈ M не ведёт ни одного ребра, кроме ребра (v, u) . Тогда u точно станет недостижима после удаления v и v является точкой сочленения. Отсюда следует, что если в M есть хотя бы одна вершина, к которой ведёт в точности одно ребро, то v — точка сочленения.

Обратное утверждение, которое заключается в том, что если в M таких вершин нет, то v не является точкой сочленения, можно доказать по индукции по размеру множества M , используя тот факт, что на входе нам дан ацикличный граф. Из доказанного выше критерия бытия точкой сочленения легко следует решение за O(m) — для каждой вершины проверить его выполнение.

Задача K. Не бабочка

Дан массив a, состоящий из n целых беззнаковых 32-битных чисел (т.е. чисел в диапазоне от 0 до 2^32 − 1), а также целое число k, кратное четырём. Для каждой позиции в массиве a i требуется вычислить следующую функцию:

1. Выписать числа ai − k+1, ai − k+2, . . . , ai −1, a i, недостающие числа следует заменить нулями.

2. Разбить выписанные числа на непересекающиеся четвёрки подряд идущих.

3. Для каждой четвёрки чисел ( a, b, c, d ) вычислить число, равное a• d− b• c. В результате получится

некоторая последовательность x1, x2, x3, . . . , xt, где t = k4 .

4. Результатом функции является число ( . . . (( x1 N AN D x2) N AN D x3) . . .) N AN D x t.

Все вычисления, описанные выше, следует производить в типе данных беззнаковых целых 32-битных чисел с переполнениями.

N AN D — операция побитового И-НЕ, также называемая штрихом Шеффера. Она определяется следующим образом: a NAND b = NOT(a AND b), где операции NOT и AND являются побитовыми, то есть применяются к каждому разряду аргументов независимо.

Формат входных данных

В первой строке записаны два целых числа n и k (4 ⩽ k ⩽ n ⩽ 10^5; k кратно четырём). Во второй

строке записан массив a (0 ⩽ ai ⩽ 2^32 − 1).

Формат выходных данных

В единственной строке выведите n чисел — результаты вычисления описанной функции для всех позиций данного массива.

Разбор

Для выполнения шага с разбиением на четвёрки достаточно решить задачу 4 раза — совершив пробеги с шагом 4 . В каждом пробеге мы должны выписать весь массив и совершить описанные в условии преобразования a • d − b • c . Теперь осталось лишь научиться пересчитывать операцию NAND на отрезке. Для начала стоит заметить, что операция NAND является не ассоциативной, поэтому нельзя предпосчитать значения её вычисления на отрезках и использовать их для техник вроде дерева отрезков. С другой стороны, рассмотрим, как вычисляется NAND для пар битов:

● 0 NAND 0 = 1

● 0 NAND 1 = 1

● 1 NAND 0 = 1

● 1 NAND 1 = 0

Заметим, что если справа стоит 0 , то независимо от левой части выражения, результатом вычисления является 1 . Для 1 же верно, что если она стоит справа, то она меняет бит, стоящий справа. Отсюда следует такое решение: чтобы посчитать функцию на отрезке, достаточно знать расстояние от правого конца отрезка до последнего 0 на нём. Если этот 0 не входит в отрезок или стоит в его левом конце, то чтобы вычислить функцию достаточно просто посчитать по модулю 2 количество операций инвертирования на отрезке, что равносильно количеству 1 после крайней левой позиции, а потом применить эту агрегированную операцию к крайнему левому биту отрезка. В ином случае количество 1 нужно считать не от левого края отрезка, а от последнего 0 , так как в этот момент результат вычисления функции обратится в 1 и до конца также будет лишь инвертироваться с каждой 1.