A. Ревизия
В пяти городах A, B, C, D и E требуется провести документальную ревизию. Для осуществления этой ревизии необходимо составить и издать приказ о ее проведении. Одним из пунктов в приказе является время командировки ревизора (лица, осуществляющего проверку в городах A, B, C, D, E).
Данная таблица содержит информацию о том, сколько времени занимает путешествие между каждым из городов.
Ревизор должен посетить каждый из городов, при этом вернуться в тот, с которого он начал свою проверку.
Так, например, маршрут A-B-C-D-E-A удовлетворяет условиям поставленной перед ревизором задачей, а длительность командировки, при таком маршруте, равна 9+27+11+20+8 = 75. Маршрут A-B-C-D-E не является правильным, так как ревизор не вернулся в город A.
Согласно данным таблицы требуется найти минимальное время командировки ревизора. Время, занимаемое проверкой в каждом из городов, не учитывать, а каждый город можно посещать только один раз.
Ответ: 65
B. Головокружительные числа
Маша – большая поклонница всевозможных кругов, кружочков и окружностей. Она старается разглядеть их во всем, что ее окружает. А еще она очень любит гармонию и математику. Не обошла она своим вниманием и числа, решив для себя, что будет считать "округлым" лишь то число, которое содержит в своей записи столько кружков, из скольки цифр оно состоит. Например, число 678 – "округлое", а 12678 таковым не является. А если еще при этом в числе в первой и последней цифре количество кругов совпадает, то это вообще "головокружительное" число. Написать программу проверки числа на "округлость" и "головокружительность".
Разбор. Нужно было аккуратно посчитать кружочки в цифрах
числа и количество цифр числа и обработать все случаи. Проблемы: возникли у
участников, которые писали решение на Питоне, входную строку нужно было
обработать при помощи int(input()) или
убрать перевод строки с помощью метода strip: input().strip().
C. Транспортировка
На складе лежат N ящиков с товарами, их веса равны 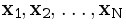 .
.
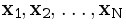 .
.
К складу подъехали две машины, чтобы доставить эти товары в магазин. Требуется загрузить ящики в эти две машины так, чтобы веса перевозимых ящиков (вес ящиков в более загруженной к весу ящиков в менее загруженной) в них отличались не более, чем в D раз. Если разделить ящики таким образом возможно, вывести Yes, иначе No.
Разбор. Известная
задача с Тимуса. Решается с помощью перебора. Можно кодировать ящики в первой
машине нулями, а ящики во второй единицами, и брать оптимальное соотношение
весов.
Жадный
алгоритм не оптимален. Попробуйте, например, распределить оптимально ящики с
весами 5 5 4 3 3 жадным алгоритмом.
D. Числа – палиндромы
Будем называть число палиндромом, если оно одинаково читается слева направо и справа налево. Например, числа 6, 232 и 1221 - это палиндромы, а число 3210 - нет. Для заданного числа N выведите первое число такого вида, которое строго больше N.
Превращаем считанное число в палиндром,
переписывая цифры из первой половины строки в обратном порядке во вторую половину
строки. Если число получилось меньше исходного — увеличиваем первую половину
числа на 1 и снова превращаем его в палиндром.
E. Подпоследовательность
Для заданного набора целых чисел найдите подпоследовательность минимальной длины, сумма элементов в которой делится без остатка на 1000000.Разбор. Известная задача. Использовалась ранее на муниципальных олимпиадах.
Рассмотрим частичные суммы элементов последовательности от
ее начала до i-го элемента
включительно. Так как нас интересуют остатки от деления
суммы на 1000000 и из свойства остатков
известно, что (X+Y) mod M= ((X mod M) + (Y mod M)) mod M,
можно рассмотреть не сами суммы, а их остатки от деления. Так как нас
интересует остаток равный 0, мы должны найти в последовательности остатков
частичных сумм ближайшие одинаковые значения (если остатки одинаковы, значит
остаток для суммы элементов подпоследовательности между ними равен 0). Для
этого для каждого остатка нужно запоминать позицию, когда этот остаток
встречался и находить минимальный вариант для разницы позиций.
F. Подпоследовательность - 2
Наибольший общий делитель двух чисел вычисляется по формуле: НОД(a,b)=a, если b=0; НОД(a,b)=НОД(b, a mod b), если b>0. НОД нескольких чисел вычисляется последовательным применением НОД к парам чисел: НОД(a,b,c)=НОД(НОД(a,b),c), НОД(a)=a.
Посчитайте, сколько различных значений принимает наибольший общий делитель для всевозможных последовательностей вида 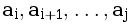 , где 1≤ i ≤ j ≤ N в последовательности
, где 1≤ i ≤ j ≤ N в последовательности 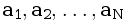 .
.
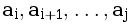 , где 1≤ i ≤ j ≤ N в последовательности
, где 1≤ i ≤ j ≤ N в последовательности 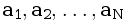 .
.
НОД подпоследовательности чисел не может
возрастать при добавлении очередных элементов в подпоследовательность и таким
образом не может принять более
log2(1018)
значений (примерно 60).
Пусть Di =
{ НОД(aj , . . . , ai ) | j ≤ i }, при этом размер Di
не превышает O(log2 (ai) ).
Тогда можно рассчитать D i+1 = { gcd(v, a i+1)
| v ∈
Di } ∪ { ai+1}
Время работы алгоритма O(N log22(1018)).

Комментариев нет:
Отправить комментарий