Разбор задач командного тура XIX открытого чемпионата Сыктывкарского государственного университета им. Питирима Сорокина по программированию

Командный тур XIX открытого чемпионата Сыктывкарского государственного университета им. Питирима Сорокина по программированию состоялся 21 апреля 2018 г. Результаты можно посмотреть здесь

А. Образование графа

Имя входного файла: стандартный ввод

Имя выходного файла: стандартный вывод

Ограничение по времени: 1 секунда

Ограничение по памяти: 256 мегабайт

Дети во многих дворянских семьях получали домашнее обучение. Александра К. обучали, кроме языков, танцев, рисования и музыки, царице наук – математике. Однажды учитель, желая надолго занять Александра, дал ему следующую задачу: расставить цифры от 1 до 9 в ряд таким образом, чтоб из любых двух стоящих рядом цифр можно было составить число, делящееся на 7 или на 13. Учитель был разочарован. Александр нашел последовательность за четверть часа. Ваша задача в том, чтобы найти какую-нибудь подходящую условию задачи последовательность и напечатать ее.

Формат входных данных. Нет.

Формат выходных данных. Последовательность из 9 цифр, напечатанных в одну строку через пробел.

Разбор

Источник: фольклор

Автор: Казаков А.

Графы (математика, ответ). Множество двузначных чисел, состоящих из различных цифр, не включающих 0, делящихся на 7 или на 13: {14, 21, 28, 35, 42, 49, 56, 63, 84, 91, 98, 13, 26, 39, 52, 65, 78}, естественным образом порождает граф. Уже глядя на этот граф, легко найти цепь, которая проходит через все вершины (наш путь не должен заходить в какую-либо вершину дважды, а вначале или в конце его стоит соответственно ⑦⑧ или ⑧⑦). Здесь вариантов решения много, например: ⑦⑧②⑥⑤③⑨④①. Годится любой.

B. Пароль

Имя входного файла: стандартный ввод

Имя выходного файла: стандартный вывод

Ограничение по времени: 1 секунда

Ограничение по памяти: 256 мегабайт

Александр любит компьютерные игры, но учитель этому не рад. Но почему бы не воспользоваться желанием поиграть в учебных целях? Итак, на вход поставлен пароль, составленный из двух чисел. Пароль составляют вместе учитель (У) и отец Александра (О). Учитель задумал сумму чисел, а отец - их произведение. Числа разные. Каждое из них больше 1, а их сумма и произведение меньше 100. Александр подслушал разговор учителя с отцом (они не очень-то скрывались):

О. Я не могу угадать эти два числа.

У. Я знал, что Вы не сможете. Но и я тоже не могу их угадать.

О. Тогда я их знаю!

У. Если Вы их можете угадать, то и я их знаю.

Этого оказалось достаточно, чтобы Александр нашел решение. Ваша задача - определить эти два числа.

Формат входных данных. Нет.

Формат выходных данных. Два числа в одной строке через пробел по возрастанию.

Разбор

Источник: Загадка про мудрецов, фольклор.

Автор разбора: Котелина Н.

Заметим, что

1. 2 простых числа заданы быть не могут. Иначе О. знал бы их.

2. У. знает сумму чисел. При этом он точно знает, что О. не может угадать эти числа, значит сумма не раскладывается в сумму 2-х простых.

Это числа: 11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53, 57, 59, 65, 67, 71, 77, 79, 83, 87.

Будем называть их списком учителя.

Из этих 2 идей  можно получить возможные пары (перебором). При этом учитываем, что сумма и произведение чисел меньше 100. Перебор всех возможных произведений сделайте сами. Из полученного списка уберем лишние числа. Для этого воспользуемся тем, что О. узнав информацию из пункта 2), догадался что это были за числа.

О. знает произведение чисел. Это могут быть числа:

18, 24, 28, 30, 41, 42, 50, 52, 54, 60, 66, 70, 72, 76, 90, 92, 96.                       (1)

 О. рассмотрел все возможные варианты разложения своего числа на 2 множителя.

 Посчитал сумму для каждого варианта и убрал все варианты, для которых сумма раскладывается на 2 простых слагаемых: После этого осталась 1 пара.  

Это значит, что если мы возьмем числа из списка (1), разложим их на всевозможные пары множителей, возьмем все  их суммы, то для каждого числа из списка (1) ровно одна сумма не разложится на 2 простых (т.е. входит в список учителя).

Значит можно отсечь лишние варианты, проделайте это сами. Получите, что все числа, которые могут быть у отца это: 18, 24, 28, 50, 52, 54, 76, 92, 96.

Назовем этот список списком отца.

Надо отсечь еще несколько пар. Как это сделать? Вспомним, что теперь и У. их знает.

У. знает сумму. У. знает список отца. Учитель знает, что отец числа знает.

Раскладываем число учителя в сумму 2-х слагаемых, рассматриваем список произведений этих слагаемых, и очевидно, что  только одно произведение должно входить в список отца (иначе отец не смог бы однозначно разложить произведение на числа, подходящие под список учителя).

Берем  список учителя 11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53, 57, 59, 65, 67, 71, 77, 79, 83, 87 и вычеркиваем из него все неподходящие:

 11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53, 57, 59, 65, 67, 71, 77, 79, 83, 87.

Остается одно число 17. Значит ответ 4 и 13.

С. Александр и драконы

Ограничение времени 1 секунда
Ограничение памяти 256Mb
Ввод стандартный ввод или input.txt
Вывод стандартный вывод или output.txt

Александр играет с учителем в математическую игру. Учитель выкладывает перед Александром n карт драконов и устанавливает начальную силу Александра равной s. Каждый дракон обладает некоторой силой (натуральное число) и здоровьем (целое неотрицательное число). Александр может брать карты драконов в произвольном порядке. Если Александр берет карту дракона и его сила не больше, чем сила этого дракона, то он проигрывает. Если же сила Александра больше, чем сила дракона, то он забирает карту дракона, а его сила увеличивается на величину здоровья этого дракона. Для победы Александру надо забрать всех драконов учителя, или, если это невозможно, сообщить учителю, сколько драконов он может забрать со своим начальным уровнем силы.

Александру стало лень считать самому и он написал программу. Вам предлагается написать свой вариант программы для решения этой игровой задачи.

Формат ввода

Первая строка содержит два целых числа, разделенные пробелом: s - сила Александра и n - количество карт (1≤s≤10⁴, 1≤n≤10³). Далее следуют n строк: i-ая строка содержит целые числа x_i и y_i (1≤x_i≤10⁴, 0≤y_i≤10⁴), разделенные пробелом — силу i-го дракона и здоровье (бонус за победу).

Формат вывода

Выведите наибольшее количество драконов, которое Александр может забрать у учителя.

Пример 1

Ввод	Вывод
2 2 1 99 100 0	2

Пример 2

Ввод	Вывод
10 1 100 100	0

Примечания

В первом примере сила Александра изначально равна 2. Поскольку сила первого дракона меньше 2, то Александр может с ним сразиться и победить его. После этого он получает бонус и его сила возрастает до 2+99=101. Теперь он может победить второго дракона.

Во втором примере сила Александра слишком мала, чтобы он мог сразиться с единственным драконом и победить.

Разбор

Источник: http://codeforces.com/problemset/problem/230/A

Заметим, что если Александр сражается с драконом, сила которого меньше силы Александра, то Александр ничего не теряет — наоборот, его сила увеличивается на целое неотрицательное число. Поэтому будем всё время выбирать какого-либо дракона с меньшей силой, чем у Александра в данный момент, и сражаться с ним. Так будем продолжать до тех пор, пока не победим всех драконов, или пока не останутся только драконы, которых Александр не может победить. Дракона на каждом шаге можно искать по-разному — как проходиться по всем драконам, так и сначала отсортировать драконов по возрастанию силы.

D. Теорема Пика

Имя входного файла: стандартный ввод

 Имя выходного файла: стандартный вывод

Ограничение по времени: 1 секунда

Ограничение по памяти: 256 мегабайт

Учитель математики Александра - очень образованный человек. Сегодня он разбирает с Александром соотношение между площадью многоугольника и количеством точек с целочисленными координатами, лежащими строго внутри и на сторонах многоугольника. Это нетривиальное соотношение открыл австрийский математик Георг Александр Пик в 1899 г. Пусть на плоскости с декартовой системой координат дан некоторый многоугольник с ненулевой площадью S. Обозначим количество точек с целочисленными координатами, лежащих строго внутри многоугольника через I, а количество точек с целочисленными координатами, лежащих на сторонах многоугольника через B. Тогда S = I + B/2 − 1. Александру требуется по известной площади многоугольника и координатам его вершин вычислить сколько точек с целочисленными координатами лежит строго внутри многоугольника.

Формат входных данных

В первой строке задано число N (3 ⩽ N ⩽ 1000) - количество вершин многоугольника, во второй строке вещественное число S - площадь многоугольника. Далее следует N строк, содержащих целочисленные координаты вершин многоугольника xi , yi , не превосходящие по модулю 106 , в порядке обхода по или против часовой стрелки (последовательно, одна за одной).

Формат выходных данных

Количество точек с целочисленными координатами, лежащих строго внутри многоугольника.

Пример стандартный ввод

4

4

-1 -1

-1 1

1 1

1 -1

стандартный вывод

1

Разбор

Источник: подобную,  но более сложную задачу можно найти по ссылке: http://informatics.mccme.ru/mod/statements/view3.php?id=1160&chapterid=456#1

Единственная сложность - найти количество целых точек на границе многоугольника. Это число получится, если сложить количества целых точек для всех ребер многоугольника. Для одного ребра с концами в точках (x1, y1), (x2, y2) это количество равно НОД(|x1-x2|, |y1-y2|) + 1. Но при сложении каждая концевая точка будет подсчитана дважды, поэтому общее количество целых точек на границе

B= Σ(НОД(|x[i]-x[i+1]|, |y[i]-y[i+1]|)).

Дальше надо применить Теорему Пика, и вывести I=S-B/2 + 1.

E. Деление с остатком

Ограничение времени 1 секунда
Ограничение памяти 256Mb
Ввод стандартный ввод или input.txt
Вывод стандартный вывод или output.txt

Учитель объясняет Александру новую тему: целочисленное деление с остатком. Чтобы закрепить тему, учитель предложил Александру поиграть. Учитель загадывает два натуральных числа x и k. Затем он сообщает Александру число k, а x не говорит. Александру надо найти остаток от деления x на k.

Чтобы Александр мог это сделать, учитель дополнительно дает Александру список из n натуральных чисел c₁, c₂, ..., c_n, и для каждого из них Александр может спросить у учителя остаток от деления x на c_i. Для данного k и списка чисел определите, сможет ли Александр узнать остаток от деления x на k для любого значения x?

Формат ввода

В первой строке входных данных записаны два целых числа n — количество чисел в списке и k, выбранное учителем (1≤n,  k≤1000000). Во второй строке записаны n натуральных чисел c₁, c₂, ..., c_n (1≤c_i≤1000000).

Формат вывода

Выведите строку “Yes”, если Александр может вычислить остаток от деления x на k для любого значения x, и “No” в противном случае.

Пример 1

Ввод	Вывод
4 5 2 3 5 12	Yes

Пример 2

Ввод	Вывод
2 7 2 3	No

Примечания

В первом примере Александр может узнать значение, потому что k = 5 является одним из чисел списка. Во втором примере Александр не может знать наверняка. Например, 1 и 7 дают одинаковые остатки при делении на 2 и 3, но разные при делении на 7.

Разбор

Источник: http://codeforces.com/problemset/problem/687/B

Разбор:  Перевод Котелина Н. , доступен на англ. языке по ссылке: http://codeforces.com/blog/entry/45770

Подсказка. Пусть ответ на тест No. Тогда должна существовать пара чисел  x1, x2 такая, что оба эти числа имеют одинаковые остатки при делении на все ci, но имеют разные остатки при делении на  k.

Решение. Пусть   x1 и  x2 - пара, описанная выше.  Тогда x1 - x2 ≡ 0   для всех 1 ≤ i ≤ n. Тогда x1-x2 делится на НОК(c₁,...,c_n) (НОК по - английски это lcm  ):

Также справедливо, что  

().

Значит, НОК(c₁,...,c_n) не делится на k:

.

Мы нашли необходимое условие.  Это условие будет также и достаточным.

Пусть , докажем, что существуют x1, x2 такие, что x1 - x2 ≡ 0 () (для всех 1 ≤ i ≤ n), и ()..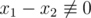

Возьмем  x1 = lcm(c1, c2, ..., cn)и x2 = 2 × lcm(c1, c2, ..., cn), тогда эта пара - искомая. Так что, остается проверить, делится ли  lcm(c1, c2, ..., cn) на  k, что можно сделать факторизацией  k и всех значений ci.

Для каждого целого  x меньшего  MAXC, найдем его gpd (наибольший простой делитель) gpdx используя решето Эратосфена sieve of Eratosthenes за .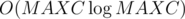

Используя массив gpd запишем  c_i=p1^q1p2^q2...pm^qm , где  pi простое число  и выполняется 1 ≤ qi . Можно выполнить это за 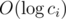  двигаясь от ci до  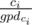и добавляя gpd(ci)  в ответ. Аналогично факторизуем k. Теперь для каждого простого  p такого, что 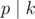, посмотрим существует ли c_i такое, что степень p в факторизации  ci   не меньше,  чем степень p в факторизации k.

F. Логический блок ИИ

Ограничение времени 1 секунда
Ограничение памяти 256Mb
Ввод стандартный ввод или input.txt
Вывод стандартный вывод или output.txt

Новое увлечение Александра - программирование. Он хочет, ни много ни мало, создать искусственный интеллект. ИИ, как известно, должен мыслить логически, и Александр решил начать с создания логического блока ИИ. Вот формальная постановка задачи. На вход подается записанное без ошибок логическое выражение следующего вида

<логическое выражение> ::= true | false | <операция>(<операнды>)

<операция> ::= not| and | or

<операнды> ::= <операнд> | <операнд>, <операнды>

<операнд> ::= <логическое выражение>

У операций and и or может быть любое число операндов, у not – только один. Требуется вычислить значение этого выражения. Например, and(or(false, not(false)),not(true)) = false.

Примите и вы участие в решении этой важной задачи.

Формат ввода

Строка, содержащая логическое выражение. Гарантируется, что оно не содержит ошибок.Количество символов в выражении не более 255.

Формат вывода

Значение этого выражения, слово true или false.

Пример

Ввод:  and(or(false,not(false)),not(true))
Вывод: false

Разбор

Источник: задачник по программированию Пильщикова, Интеллектуальный марафон 2010, ФМЛИ.

Преамбула. Известный польский логик и философ Ян Лукасевич известен во всем мире как один из наиболее выдающихся и значительных логиков ХХ столетия и, прежде всего, как создатель первого исчисления многозначной логики. Им также была разработана система логической символики, известная под именем польской нотации (записи). Это префиксная запись логического выражения, в которой знак операции стоит перед операндами. Польская запись не используется в математике, но широко применяется в информатике.

Выполнить лексический разбор выражения представить в постфиксной форме и провести вычисления, например, используя конечные автоматы и стек. 

const n = 255;

var c: char;

    st: array[1.. n] of char;

    top: integer;

    ex: array[1.. n] of boolean;

    tb: integer;

procedure push(c: char); {затолкнуть в стек}

begin

    inc(top);

    st[top] := c;

end;

function pop: char; {вытолкнуть из стека}

begin

        pop := st[top];

        dec(top)

end;

var b: boolean;

begin

       

        top := 0;

        while not eof do begin

        read(c); {первые буквы всех операций разные, по ней и делаем разбор}

        case c of

          'a': begin push(c); read(c); read(c); read(c)  end;

          'n': begin push(c); read(c); read(c); read(c)  end;

          'o': begin push(c); read(c); read(c)  end;

          't', 'f': begin push(c); repeat read(c) until c = 'e' end;

          ')'     : begin  tb := 0;

                           c := pop;

                           while (c = 't') or (c = 'f') do  begin

                                inc(tb);

                                ex[tb] := c = 't';

                                c  := pop;

                           end;

                           case(c) of

                           'a': begin

                                b := true;

                                while tb > 0 do begin

                                   b := b and ex[tb];

                                   dec(tb)

                                end;

                                end;

                           'o': begin

                                b := false;

                                while tb > 0 do begin

                                   b := b or ex[tb];

                                   dec(tb);

                                end;

                                end;

                           'n': begin

                                   b := not ex[tb];

                                   dec(tb)

                                end;

                           end;

                           if b then push('t') else push('f');

                   end;

        end;

        end;

        writeln(st[top] = 't');

     end.

 G. Инверсия

Ограничение времени 2 секунды
Ограничение памяти 256Mb
Ввод стандартный ввод или input.txt
Вывод стандартный вывод или output.txt

Инверсией в перестановке p называется всякая пара индексов i, j такая, что 1≤ i и p[i] > p[j].

У отца Александра есть хобби: изобретательство. Последнее его изобретение - автомат, который может генерировать случайную перестановку из чисел от 1 до n и определять количество инверсий на некотором отрезке этой последовательности. Автомат имеет дисплей для вывода чисел и два манипулятора. Первый манипулятор задает n - длину перестановки, второй задает k - количество выводимых на экран чисел, являющихся инверсиями сгенерированной подстановки. Точнее, автомат генерирует случайную перестановку из чисел от 1 до n, а потом выводит на экран n-k+1 чисел, причем i-е из этих чисел обозначает количество инверсий сгенерированной перестановки на отрезке с i по i+ k-1.

Учитель Александра экспериментирует с автоматом. Он задал n и k, и теперь требует от Александра определить, какую перестановку сгенерировало устройство. Помогите Александру.

Формат ввода

В первой строке содержатся два натуральных числа n и k (2≤ n ≤10⁵ , 2≤ k ≤5, n≥ k). Во второй строке даны n-k+1 чисел, выведенные на экран устройством. Гарантируется, что устройство исправно, и существует хотя бы одна перестановка, по которой можно генерировать эти числа.

Формат вывода

Выведите n чисел, разделенных пробелами — сгенерированную устройством перестановку. Если возможных перестановок несколько, то выведите любую.

Пример

Ввод
3 2
0 1
Вывод
2 3 1

Разбор

Источник. Двадцать первый командный чемпионат школьников Санкт-Петербурга по программированию Санкт-Петербург, НИУ ИТМО, 27 октября 2013 года.

Задача I. Необычный экспонат

Идея. Переберем, форму какой перестановки имеют первые k − 1 число ответа. Например, последовательность 100, 500, 239, 17 имеет форму 2, 4, 3, 1. Попробуем построить подходящий под эту форму ответ.
Пускай что-то известно про первые m чисел (изначально, m = k − 1). Выясним что-нибудь про очередное число. Будем строить граф G. В G есть ребро i → j, если известно, что в строящемся массиве ai < aj . Про каждую пару из {am−k+1, am−k+2, . . . , am} известно, какой элемент из пары максимальный. Перебрав k вариантов того, как будет соотноситься с ними am+1, посчитаем количество инверсий на отрезке am−k+2..m+1 в каждом из этих случаев.
Получим нужное число инверсий не более, чем в одном из случаев. Не получили ни в одном — переходим к следующей форме. Получили одно — переходим к следующему m. По условию задачи хотя бы для одной формы дойдём до конца. Запустим алгоритм топологической сортировки на получившемся графе. Полученная перестановка и будет ответом.
Полностью разбор здесь: http://docplayer.ru/64272782-Xxi-komandnaya-olimpiada-shkolnikov-sankt-peterburga-po-informatike-i-programmirovaniyu-27-oktyabrya-2013-goda.html